Sitting behind one of three doors in front of you is a brand new luxury car. You are a contestant on the iconic game show Let’s Make a Deal hosted by the charismatic Monty Hall, and you have a rare once-in-a-lifetime opportunity to win the car of your dreams. Unfortunately for you, two of the three doors contain a goat—one of the last things you would want to win. Since you’re familiar with the style of the game show, you know that the host Monty Hall is aware of which door the car is secretly behind. It is time to place your guess and possibly win it all.

   Whether you won your dream car or not, there is a puzzle hidden inside this game show, which is often referred to as the Monty Hall problem. The burning question: is it in the contestant’s best interest to stay or switch? When most people are presented with that choice, they automatically believe that their choice has no statistical significance. Since it’s 50/50 anyway, people tend to stick with their gut and stay with their original door. Plus, if you had the right door at first and switched away from it, the loss would feel much more painful.

   However, that thinking is flawed. The true probability of winning if you stay with your initial pick is only 1/3, while the chances of winning if you switch are 2/3. This appears to defy all logic: how is it possible that the other door is twice as likely to have the car behind it? The answer lies in the behavior of the host. There are three assumptions for how the host will act in order for the uneven probabilities to hold true.

1. The host must always open a door that was not picked by the contestant.
2. The host must always open a door to reveal a goat and never the car.
3. The host must always offer the chance to switch between the originally chosen door and the remaining closed door.

   Assuming those three conditions are met, the long-term probability of winning if the contestant switches will be around 66.7%. That doesn’t mean that switching is a guaranteed victory for the contestant because they will still lose a third of the time, but switching is the best decision to make without any further knowledge.

   Any time the contestant picks a door, the host will always reveal a different door with a goat behind it. We can all agree that the chances of guessing the correct door at first are 1/3 before the host reveals anything. Since the host will reveal a door with a goat behind it regardless of whether your pick is correct or not, the initial 1/3 probability for the original guess remains unchanged. That means all the remaining probability concentrates into the door the contestant didn’t pick, causing the probability of it containing the goat to become 2/3. Below is a chart to help visualize all the outcomes.

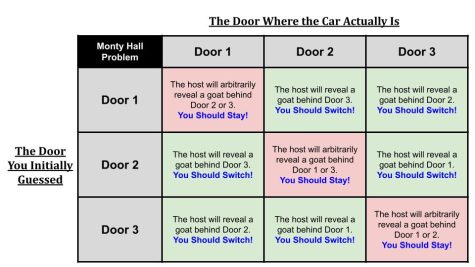
   As the figure shows, switching is the right choice for the contestant 2/3 of the time. In case this problem still seems impossible, perhaps it would be helpful to consider an exaggerated version of the puzzle. Imagine there were 100 doors, only one of which has a car behind it. Once the contestant selects a door, they will only have a 1/100 chance of getting it right. The host, knowing where the car is, will always reveal 98 of the doors with goats behind them no matter what the contestant’s initial pick was. There will still be one door remaining that the host suspiciously chose not to open. Therefore, it stands to reason that the contestant should always switch away from their original guess; after all, their odds are still at 1/100. All the probability from the 98 doors that the host revealed concentrates into the remaining door, not the door the contestant guessed. Switching in this case will allow the contestant to win 99% of the time. While this problem makes more intuitive sense with 100 doors, the exact same logic applies when there are only three, like in the game show.

   If you are still feeling a little perplexed, there is no need to worry. The Monty Hall Problem is notorious for stumping people from all walks of life, including but not limited to mathematicians with PhDs. Even with detailed explanations, computer simulations, and formal mathematical proofs, some very intelligent people do not accept the solution. Even Paul Erdős, one of the greatest mathematical minds of the 20th century, was unconvinced that the probabilities were unequal until he was shown a simulation that definitively confirmed it. There is a breathtaking amount of complexity in a problem that appears so simple at a first glance.